|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Ответить... Обсуждения... Странные у вас суждения о золотом сечении. если чуть чуть прямоугльник отличается от квадрата, значит он уже близок к золотому сечению. Бред. Я всегда считал, что пиксель квадратный. С чего вы взяли, что это круг? Уважаемый Владимир Пахомов!
Поделитесь, пожалуйста, секретом, как Вы отличаете "набор слов" от "не набора слов". Если Вы хотите объективно без эмоций разобраться в "скудоумии местных архитекторов", то советую Вам почитать статью А.Ложкина "Почему в Новосибирске плохая архитектура" (на этом же сайте). Знаете ли Вы, что в хрущевских пятиэтажках "хорошие архитекторы" из ЦНИИЭПжилища проектировали с применением золотых пропорций. Если Вы думаете, что золото помогает автоматически находить наиболее оптимальные функционально-планировочные решения, то Вы ошибаетесь. Еще академик архитектуры И.Жолтовский говорил, что если тухлую колбасу разрезать в золотом сечении, то от этого она не станет свежей. Прочитал я статью А.В.Радзюкевича. Этот набор слов составлен по известному принципу - "Всё не так!". Этот принцип прекрасно изложен в известных детских стихах - "Что не делает дурак, всё он делает не так...". Сюжет там простой. Пока дурак пытался что-то делать сам - все видели, что он дурак. Когда он стал критиковать других, некоторые стали считать его умным. Недавно я читал эту сказку моей внучке, она поняла.
Если диссертация пустая, то может хоть оппоненты что-нибудь напишут - в этом весь смысл "дискуссий", лишённых предмета обсуждения. В России, каждый человек испытывает на себе скудоумие местных архитекторов. Посмотрите на свой дом, посмотрите на планировку своей квартиры - какой урод мог спроектировать такое? Посмотрите, как новосёлы затаскивают мебель на последний этаж дома и спросите их - что они думают об "архитекторах", придумавших такие лестничные клетки. Посмотрите на молодых мам, гремящих детскими колясками по ступеням лестниц, лишённых специального спуска. Спросите инвалидов, которых "архитекторы" лишили возможности самостоятельно выбраться на улицу. Если "учитель архитекторов" А.В.Радзюкевич не понимает принципа и использования "золотого сечения", то это его проблемы. Наверное и поэтому, дипломы местных архитекторов не признаются в других странах. Владимир Пахомов По ГОСТовским чертежам отступ от края листа с 3 сторон равен 5 мм, а с четвертой стороны 20 мм. Где тут дюйм? где тут ЗС? Уважаемый Борис Резин!
Еще один вопрос вдогонку. Вы пишете, что "если измерить победителей конкурса красоты, то их пропорции будут гораздо ближе к ЗС". Вы в это ВЕРИТЕ или Вы это ТОЧНО ЗНАЕТЕ? Уважаемый Борис Розин!
Никто не обещал никому, что пиксел есть идеальная окружность. А какая это фигура? Я взял линейку и проверил размеры моего монитора. Получилось примерно 32,5см на 24,3см (пропорция 1,33744...). Где же тут "золото"? По поводу формата бумаги. Сколько готовлю документы по ГОСТУ (чертежи и тексты) ни разу не встречал требования о том, что поля по всем стронам должны быть равны дюйму. Подскажите номер ГОСТа. При этом, при чем тут поле текста? Формат бумаги нарезают в корнеквадратном соотношении в связи с простейшим практическим удобством. В листе формата А-3 содержится два листа формата А-4. В листе формата А-2 содержится два листа формата А-3 (или 4 листа формата А-4). И так далее. При этом, пропорции листов А-4, А-3, А-2 (и т.д.) одинаковы. При чем тут поле текста? Насчет пластиковых карточек ничего не скажу. В США не был. В Росии не завел. Даже если национальный стандарт пластиковых карточек в США имеет соотношение сторон 1,59, то возникает вопрос - а почему не 1,618? Отчего такая небрежность? Уважаемый Андрей Владиславович,
Не дожидаясь завтра, отвечаю. Разрешающая способность монитора не связана напрямую с пропорциями экрана монитора. Соотношение количества точек по горизонтали и вертикали соответствует частоте кадровой и срочной разверток телевизионной трубки. Если помните стандарт EGA предполагал разрешение 640х200, а популярный ныне формат 1280х1024. Числа в формате монитора показывают количество точек (пикселей) по горизонтали и вертикали, но никто не обещал нам что пиксел это идеальная окружность. Самый распространенный формат бумаги А4 (11,5”x8”). Если помните требования ГОСТ для техдокументации – поля шириной 1” (2,5 см) c четырех сторон. Тогда поле для текста будет иметь размер 9,5”x6” или пропорцию 1,583, отклонение от 1,618 - 2%. Не знаю как в России, а в США используются бизнес-карты размером 2”x3,5” (5,12x8,96 см) и 2”x3,25” (5,12x8,32 см), пропорции последней 1,625. А национальный стандарт пластиковых карт 2-1/8” x3-3/8” с соотношением сторон 1,59. С уважением, Борис Розин Борис Розин, кто такой ЛеКобюзье? Уважаемый Борис Розин!
К сожалению, у меня сечас нет времени на развернутый ответ. Но прошу Вас пока проверить правильность Ваших же утверждений на простом примере. Формат монитора равен 800 на 600 точек, либо 1024 на 768 точек, либо 1152 на 864 точки и т.д. Во всех случаях имеем соотношение 4 на 3. (или у Вас какой-то другой монитор?). Формат визитной карточки - 9см на 5см. Все стандартные форматы бумаги дают корнеквадратное соотношение сторон. Никакого золотого сечения здесь нет. Если же предположить, что эти пропорции примерно близки золоту, то тогда действительно можно утверждать, что золото есть везде. Завтра я постараюсь вернуться к обсуждению Ваших замечаний. Уважаемый автор!
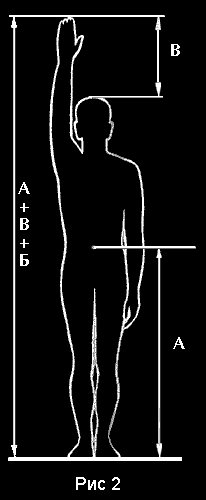
Вы можете провести со своим студентами простенький эксперимент. Возьмите чистый лист бумаги, желательно формата А4, и проведите посредине вертикальную линию. Затем добавьте несколько симметричных отрезков, под углом 45 градусов из вертикальной линии вниз, так, что бы получилось некоторое подобие елочки. И предложите студентам провести линию горизонта. Любой человек, обладающий некоторым интуитивным чувством красоты, а тем более учащийся архитектурно-художественной академии, никогда не проведет ее по середине листа. Линия горизонта будет «сдвинута» либо немного выше либо немного ниже. Это «немного» и есть сущность ЗС. Важно то, что ЗС, как пропорциональное соотношение частей в целом, не равно ½ (0,5). И так, ЗС связанно с человеческим восприятием, т.е. с точки зрения «чистой науки» явление субъективное. Однако, если этим «субъективным восприятием» обладают подавляющее большинство людей, то мы должны его рассматривать как объективное явление. Архитектура, как и другие бытовые произведения человека, является преобразованием окружающей среды для своих потребностей. Рассмотрим процесс интуитивного творчества: Человек смотрит. Поле ясного зрения, в глазном дне человека, имеет форму эллипса, оси которого относятся как α [1]. Поэтому предметы, в форме которых содержится ЗС воспринимаются «благоприятно». Это объясняет опыт с елочкой и опыты Фехнера. Не напрасно всеми нами любимые экраны TV и компьютеров, а также кредитные карточки имеют соотношение длины и ширины равное золотой пропорции. Человек думает. А.А.Соколов и Я.А.Соколов, в работе [2], показали, что соотношение частот волн (ритмов) электрических колебаний мозга равно ЗС. Мозг принимает решения по алгоритму ЗС. Человек делает. В исследованиях Цейзинга [3] и Хембиджа[4], которые подтверждены в наше время Дочи[5], Петуховым[6] и Шапаренко[7], показано наличие золотой пропорции в отношении частей тела человека, в частности руки. Можно сказать, что мастер всегда имеет эталон золотой пропорции "под рукой". Произведения человека является отображением окружающего мира через цепочку глаз-мозг-рука. Каждый из элементов этой цепочки содержит золотую пропорцию в своей внутренней структуре. В процессе созидания, происходит трехкратный "резонанс" ЗС по цепочке глаз-мозг-рука. Вы можете задать несколько правомерных вопросов: 1. Почему нас окружает так много «некрасивых» вещей и сооружений? К сожалению функциональность, технологичность и удешевление часто сводят на нет интуитивные устремления автора. 2. Почему размеры картин не соответствуют пропорциям ЗС? Не размеры картин важны, а композиция, расположение информационно-узловых точек (см. [1]). 3. Почему статистические антропометрические измерения не попадают в ЗС. Многое зависит от того кого и как измерять. Если измерить победителей конкурса красоты, то их пропорции будут гораздо ближе к ЗС. Это относится к мужчинам, для женщин инвариант пропорций несколько отличается от 1,618. 4. Как древний архитектор, без компьютера, мог построить ЗС? Очень просто, при помощи только циркуля и линейки. Диагональ двойного квадрата равна корню из 5. 5. Зачем ЛеКобюзье добавил в Модулор неподтвержденную антропометрическими исследованиями последний шаг с «вытянутой рукой»? Оставим это на совести ЛеКобюзье. 6. Почему ЗС встречается не только в произведениях человека, но и в живой природе? Потому, что ЗС является функциональным признаком самоорганизующихся систем. Подробней смотрите мою работу «Золотое сечение: морфологический закон живой природы.» на сайте www.goldensection.net И последний вопрос. Почему апологеты ЗС не могут представить неопровержимых доказательств его существования? Приблизительно тот же вопрос задавали сторонникам шарообразной формы Земли. «Покажите место где Земля закругляется. Если такого места нет, значит она плоская, а шарообразность это красивая сказка.» Прошли века, человек оторвался от Земли и увидел, что она не шар, а нечто более сложное. С уважением, Борис Розин www.goldensection.net , rozinb@yahoo.com 1. Ковалев Ф.В. Золотое сечение в живописи/ Учебное пособие.-К., 1990. 2. Соколов А.А., Соколов Я.А. Математические закономерности электрических колебаний мозга.-М., 1977. 3. Zeising A. Neue Lehre von den Proportionen des menschlichen Korpers. Leipzig, 1854. 3. Хембидж Д. Динамическая симметрия в архитектуре.-М,. 1936. 5. Doczi G. The power of limite. Proportional harmonies in nature, art and architecture.-London, 1981. 6. Петухов С.В. Биомеханика, бионика и симметрия.-М., 1984. 7. Шапаренко П.Ф. Принцип пропорциональности в соматогенезе.-Винница, 1994. С интересом прочитал статью Радзюкевича А.В. "Красивая сказка о золотом сечении". И надо сказать, согласен с выводами статьи. И не так важно, кто автор статьи, и вправе ли он замахиваться на правомерность существования "божественной пропорции", статья не об этом. Вопрос поставлен верно. Вправе ли мы так вольно обращаться с математическими константами, и не подменяем ли мы действительность нашими умозрительными образами? Так ли на самом деле, или просто нам так хочется….
К сожалению "мода" в науке столь же сильна, как и жизни. Приходит время, … и все начинают примерять на себя новый "наряд", какую-нибудь новомодную теорию или открытие. Оно к нашим трудам и отношения не имеет, но вдруг становится совершенно необходимым… К сожалению, так было всегда. Посмотрите на физические формулы из разделов "электричество, магнетизм". Одинаковые, как близнецы. И дело не в схожести действия, дело в "моде" того времени. Может быть, сегодня, эти же формулы были бы изложены иначе, не знаю… Конец 19 века и начало 20 -го было временем расцвета науки. И не только науки, но и всяких "околонаучных" теорий. Революция идей. Все генерировали идеи. Пусть не всегда научные, да кто бы разбирался… Раскопали Трою - Ура! И по сей день спорят, Троя это или нет? Но это уже не важно… Тогда же "откопали" и Божественную пропорцию. В условиях расцвета спиритизма и поиска древних богов это более чем отвечало духу времени. В архитектуре появилась своя древняя пропорция… Теперь можно не "на глазок", и не "красиво или нет", теперь можно проверить и на соответствие древней божественной пропорции… Математическое выражение красоты - идеал не только архитектуры, но и искусства во всех его проявлениях. Вот тут и вмешалась "мода". О золотом сечении стали говорить и писать все. И пытаться применять и прикладывать ко всему, что рядом… Прошло время. Теперь бы разобраться, что так, а что не так. Но уже столько написано и такие громкие фамилии авторов, что на первое место вышла "честь мундира". Неужели можно ставить под сомнение высказывания Ле Корбюзье или Эйнштейна? А кто такой А. Эйнштейн в архитектуре? На чем основан Модулор? Золотое сечение, как и любая математическая константа обязательно отыщется в любом материальном проявлении Природы. И найдется процесс, в котором она будет доминирующей. Но, как и другие константы, она - предел множественности отклонений. Среднее теоретическое значение. Кто сможет отменить филлотаксис, если он подтвержден массой объективных измерений? Это математическое выражение объективности законов развития. Но вот объективность "гармонии и красоты" этого процесса с точки зрения архитектуры и искусства, это уже понятие не совсем научное. Мы восторгаемся пчелиными сотами, но вот жить в доме, построенном на этом принципе, что-то не всем хочется… Понятия "красоты и гармонии" меняются. Сегодня нам лучше так, завтра - иначе. Что сегодня модно, то и красиво. К сожалению. Вот только времена меняются… Усреднение всегда ведет к шаблону. Так проще. Если свести все к Золотому сечению, кто от этого выиграет? С другой стороны, а было ли такое гармоническое начало в архитектуре и искусстве изначально? Не сами ли мы его себе придумали? От минутного увлечения новой математической константой… Андрей Никитин -- Best regards, Никитин mailto:nikitin@volgodonsk.ru Уважаемый Александр Георгиевич!
Благодарю Вас за Ваш отзыв. По поводу филлотаксиса полностью с Вами согласен. Это факт безусловный. В момент написания этой статьи я полагал, что этот факт имеет только эмпирическое подтверждение. В прошлом году я попытался более детально разобраться в этой проблеме (Щетников А.И., Радюк М.С, Cohn D, Douade S., Couder Y). Мне нужно время, чтобы понять механизм возникновения этой закономерности - я не математик. Обязательно прочитаю Ваши работы. Спасибо. Сейчас мало кто из архитекторов пользуется золотым сечением. Восновном все полагаются на свой собственный глаз. Золотое сечение остается в теории. Я, пожалуй, разделяю точку зрения Радзюкевича в отношении проявленй золотого сечения в архитектуре и искусстве, поскольку не вижу для таких проявлений рациональных оснований. Основанием для использования этого отношения в указанных областях мог бы быть какой-то полузабытый в настоящее время практический способ разметки при проектировании или строительстве. Однако я решительно не согласен с отрицанием проявления ряда Фибоначчи, а следовательно и отношения золотого сечения, в филлотаксисе. Это легко наблюдаемый факт факт. Природа этого проявления также ясна. О ней, в частности, можно прочитать в моих журнальных статьях и опубликованных материалах конференций, список, котоых я прилагаю ниже.
1. Малыгин А.Г. Структурная теория филлотаксиса. I. Механизм образования спиральных структур очередного филлотаксиса. Биофизика. Т.43, №2, 1998, сс.335-342. 2. Малыгин А.Г.Структурная теория филлотаксиса. II. Взаимоотношение между низшими и высшими формами филлотаксиса. Биофизика Т. 45, № 6, 2000, сс.1112-1118 3. Малыгин А.Г. Теория филлотаксиса. I. Геометрическая модель образования спиральных форм очередного филлотаксиса. Онтогенез. Т.32, №5, 2001, с.393-400. 4. Малыгин А.Г. Теория филлотаксиса. II. Кристаллографическая интерпретация взаимосвязи между низшими и высшими формами филлотаксиса. Онтогенез. Т. 33, № 6, 2002, с.471-478. 5. Малыгин А.Г. Использование закономерностей ряда Фибоначчи для построения общей теории филлотаксиса. Сборник докладов XII симпозиума: "Перестройка естествознания в третьем тысячелетии". Москва, 20-22 апреля 2001 г. сс.83-84, 2003. 6. Малыгин А.Г. Механизм адаптивных изменений филлотаксиса в рамках реализации онтогенетической программы растений. Материалы V междунгародного симпозиума "Новые и нетрадиционные растения и перспективы их использования." Москва-Пущино, 9-14 июня 2003 г., т. III, сс.104-107, 2003. 7. Малыгин А.Г. Аксиоматическая теория филлотаксиса. Труды объединенной международной конференции "Новая геометрия природы." Казань, 25 августа-5 сентября 2003 г., т. II, сс.209-218, 2003. 8. Малыгин А.Г. Аксиоматический подход к разработке теории образования спирального филлотаксиса. Збiрник наукових праць Винницького державного аграрного унiверситету. "Проблеми гармониii, симетрii i золотого перетину в природi, науцitта мистецтвi. Вiнниця сс. 228-231, 2003. С уважением А.Г.Малыгин << 12 13 14 15 16 17 18 19 20 21 22 |

| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
www.SibDESIGN.ru
|
|